I played the violin throughout my high school life and now I play the bass, but I never questioned until now how octaves sound the same despite having different pitches. How do we recognize that the higher A is the “same” sound as the lower A?
If we look at the science of sound, we learn that sounds are a form of energy that travels through a medium such as air, water, or solid objects as vibrations of particles. These vibrations of particles in a medium come across as sound waves. Without any medium, there is nothing to vibrate, no waves to travel, and no sound to hear. This is why sound does not travel through a vacuum or in the emptiness of space. (The fact that sound needs a medium to travel through is the reason why it is slower than light. Light does not need any medium to travel and it passes through space!)
Okay, back to the sound waves, and this is where it gets interesting. Let us recall that waves have frequencies.
Frequency is the number of cycles a sound wave passes a point in a given time. The unit is Hertz (Hz), and 1 Hz is equivalent to 1 cycle of wave (in this case, sound wave) per second. A certain value of frequency constitutes a specific sound, and that’s how we hear different pitches — through different frequencies of vibrations. So, when we hear A4, that’s just us perceiving a wave that has a frequency of 440 Hz (in standard tuning). If the frequency gets slightly above 440 Hz, we hear a slightly sharp A4. Get it a little higher to reach exactly 466.16 Hz and we hear a perfect A4#. Get it up to exactly 493.883 Hz and we hear the next semitone which is B4. This shows that the difference in pitches of sound is just varying frequencies. How did I get the exact values of frequencies in my example? Don’t ask me, I just googled it.
The point is that the higher the frequency, the higher the pitch we hear. The lower the frequency, the lower the pitch.
Now, if frequencies are higher for higher pitches, then A5 must have a higher frequency than A4. Yes, that’s obvious. But then, how are they the same to our ears? Let’s look at the numbers.
A5 has a frequency of 880 Hz. That is exactly double the frequency as A4’s 440 Hz. Double 880 Hz and we get A6 which has a frequency of 1760 Hz, and so forth. The pattern that becomes apparent is that notes that are an octave apart have frequencies where the higher pitch has twice the frequency of the lower pitch. This is true not only in A, but in every note.
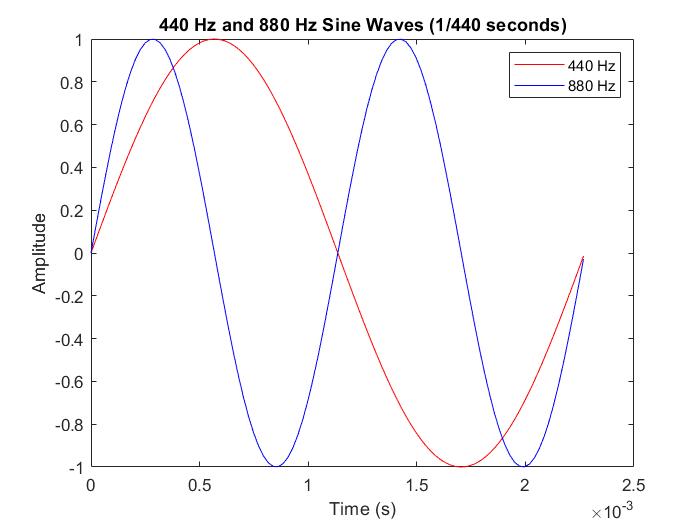
Numbers are boring. Let’s see the waveforms. Consider a 440-Hz wave on top of an 880-Hz wave. We see that exactly two cycles of an 880-Hz wave occur as one cycle of a 440-Hz wave takes place within the same time frame (1/440 s or 2.27 ms). From another perspective, we see that a full cycle of the 880-Hz wave is only a half-cycle of the 440-Hz wave. The point in time (1/880 s or 1.13 ms) when the 880-Hz started its second cycle was when the 440-Hz began its second-half cycle, both at 0 amplitude. I cannot make any more objective mathematical reasoning out of it, but by looking at these waveforms, I can judge that they are in the same harmonic pattern. They do not contradict or disturb each other. It’s like they are dancing gracefully to a song that only they understand.
Still, knowing all these physics and patterns does not answer the question of why octaves sound the same to our ears.
I think that physics alone cannot answer this because it is only one-half of the picture. We detect these waves through our ears and our brain processes it as the sound that we “hear”. I think that the brain has a huge responsibility (and its own mysteries) in the science of sound, so there’s a lot more explaining to do here. Unfortunately, this is well beyond my area of knowledge and this is where I say, I don’t know.
But I will find out and will be back to update this when I get promising answers.